martes, 18 de noviembre de 2014
DEFINICIÓN
ELIPSE
- . ELIPSE que significa una deficiencia, se utilizaba cuando un rectángulo dado debía aplicarse a un segmento dado y resultaba escaso en un cuadrado.
Una definición intuitiva de la elipse sería la siguiente: "Una elipse es una curva ovalada que se asemeja a un círculo alargado". Una definición más precisa sería la siguiente:
"Una elipse es el conjunto de todos los puntos en un plano cuya distancia a dos puntos fijos en el palo tienen una suma constante. Los puntos fijos son los focos de la elipse. La recta que une los focos es el eje focal. El punto sobre el eje focal que está en el punto medio entre los dos focos es el centro. Los puntos donde la elipse interseca a su eje son los vértices de la elipse.

HIPÉRBOLA
Es un conjunto de puntos con coordenadas (x,y) en un plano cartesiano cuya diferencia de sus distancias a dos puntos fijos colineales en el plano es constante. Estos puntos fijos reciben el nombre de focos de la hipérbola, y la línea recta sobre la cual están localizados los focos recibe el nombre eje focal o eje mayor. El punto medio entre los focos, de coordenadas (h,k), recibe el nombre de centro y a los puntos donde la hipérbola interseca al eje focal se les denomina vértice. A la recta que pasa por el centro, y que es perpendicular al eje focal, recibe el nombre de eje conjugado. A las dos curvas que forman la hipérbola se les llama ramas. La hipérbola tiene dos rectas inclinadas denominadas asíntotas, a las cuales las ramas de la hipérbola se acercan sin interceptarlas y que facilitan o sirven como guías para graficarlas.

CIRCUNFERENCIA
La circunferencia podemos definirla como una línea curva cerrada que consta de la sucesión de puntos equidistantes de un punto llamado centro. El término equidistar significa que están a la misma distancia. Los puntos de la circunferencia y los que se encuentran dentro de ella forman una superficie llamada círculo.
Ecuación general de la circunferencia:

PARABOLA
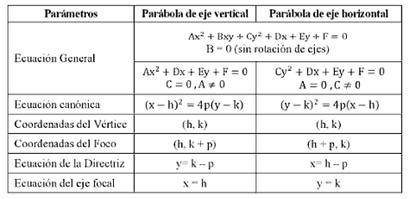
Denominamos parábola al lugar geométrico de los puntos del plano que equidistan de un punto fijo, llamado foco, y de una recta fija llamada directriz. Entonces la parábola es el conjunto de puntos del plano que está a la misma distancia de un punto, su foco, y de una recta fija, su directriz

La distancia entre el foco y la directriz de una parábola recibe el nombre de parámetro de la parábola (suele denotarse por p). Dada una parábola, se llama eje de la misma la recta que contiene al foco y es perpendicular a la directriz. Se llama vértice de la parábola al punto donde ésta corta a su eje.
Suscribirse a:
Comentarios (Atom)
